Activation/weight smoothing (SmoothQuant)#

Quark supports through quark.torch a pre-processing step called SmoothQuant, introduced in SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models. Other libraries (for example, Brevitas) sometimes refer to SmoothQuant as activation equalization.

The key idea of SmoothQuant is to apply a non-destructive rescaling on the weights and activations in order to balance out the distribution of the two. This means that SmoothQuant can be applied on a model alone, without quantization, and the model outputs would be identical to the original output.

This is for example useful when later applying quantization, where the quantization difficulty is effectively then balanced between weights and activations, which typically results in better quantization results than without applying this pre-processing step.

How does SmoothQuant work?#

Let’s take a linear layer, say

\[y = xW\]

where \(x\) is an activation of shape (batch_size, in_features) and \(W\) is a weight of shape (in_features, out_features).

This is equivalent to

\[y = (x \frac{1}{s}) \times s^TW\]

where \(s\) is called a called the scaling factor, which is a scalar or of shape (1, in_features).

As weights are frozen/fixed at inference time, the scale \(s^T\) can be fused ahead of time into an updated weight \(W' = s^TW\).

For activations, the scaling factor \(\frac{1}{s}\) can be fused into a frozen preceding layer (quark approach), or in the worse case added as a pointwise mul node in the graph.

In practice, for transformer-based networks, SmoothQuant is easily applied on the QKV projection, as well as on the first linear of the MLP (multi-layer perceptron) layer, as seen on the figure below. SmoothQuant may be applied on some other linear layers, for which special care needs to be taken when fusing the activation scale in the preceding layer:

Linear1 -> activation -> Linear2: This works well if the activation is pointwise linear (which may not be the case). Note however that the fusing of \(\frac{1}{s_2}\) into Linear1 weight might compromise its quantization.
Linear1 -> any linear op -> Linear2: The fusing of \(\frac{1}{s_2}\) into Linear1 weight might compromise its quantization.

SmoothQuant implementation in Quark supports these cases as well.

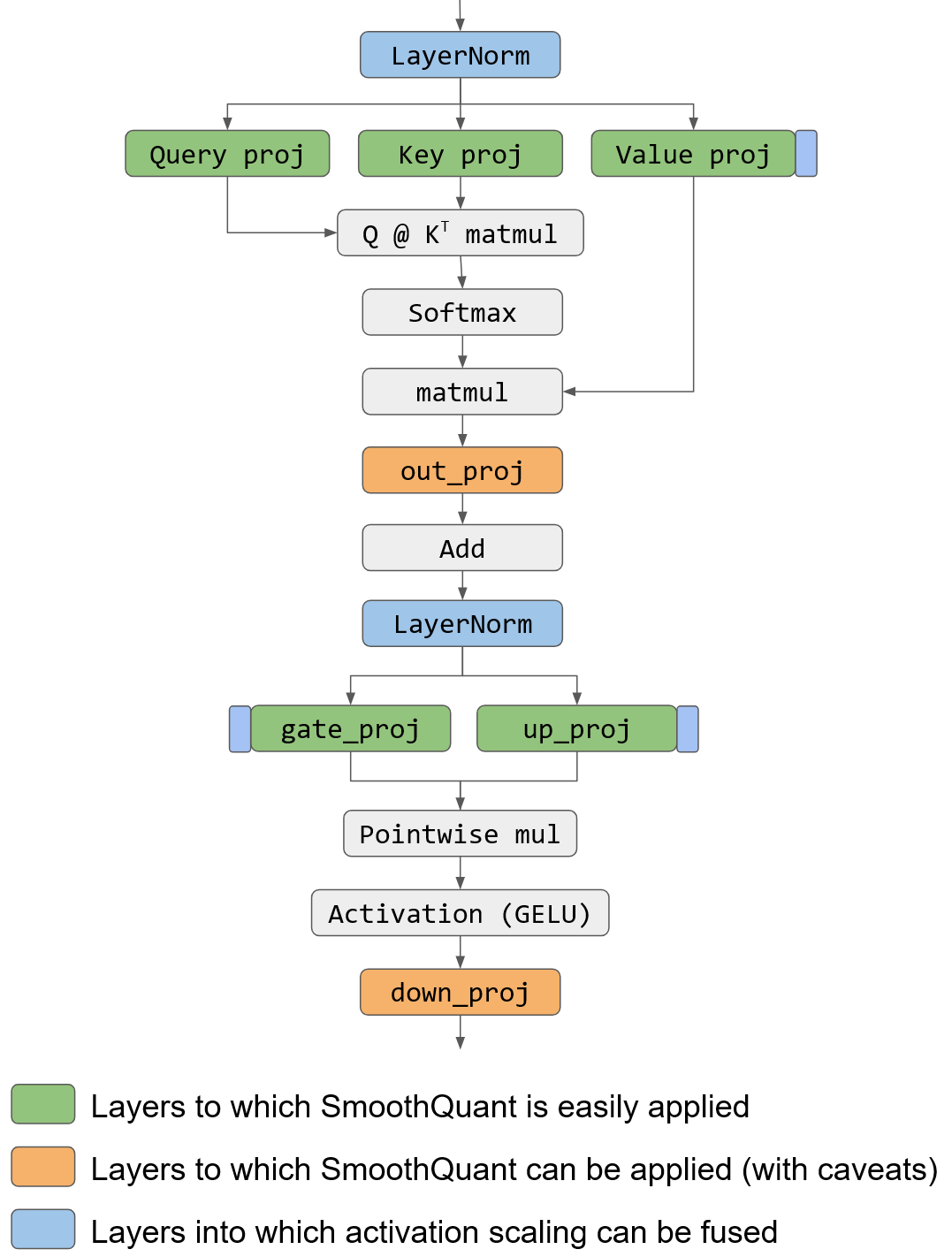
../_images/llama.png — Simplified transformer architecture (based on llama), with SmoothQuant applied.#

If quantization is applied after this pre-processing, effectively the quantized tensors will be \(W' = s^TW\) and \(x' = x \frac{1}{s}\), which may have a distribution less sensitive to quantization due to the rescaling.

The scaling factor is defined as:

\[s = \frac{max(|x|)^\alpha}{max(|W|)^{(1 - \alpha)}}.\]

Typically, the scaling factors are determined by using a calibration dataset that is run through the model in order to collect activation statistics.

Tip

SmoothQuant has an hyperparameter alpha that specifies the balance between the quantization difficulty into weights and into activations.

When weight-only quantization is used after smoothing, alpha = 0.0 is recommended to shift all the quantization difficulty from the weights into from the activations.
When activation-only quantization is used after smoothing, alpha = 1.0 is recommended to shift all the quantization difficulty from the activations into the weights.
When both weights and activations are quantized after smoothing, alpha must be tuned, but SmoothQuant paper typically recommends a value between 0.4 and 0.9 depending on the model.

In fact, we can verify the idea that SmoothQuant helps with lowering the output quantization error on a minimal dummy example that uses a single Linear layer, and a single LayerNorm to fold the activation scaling into.

import torch
import torch.nn as nn
import copy
from torch.utils.data import DataLoader

from quark.torch import ModelQuantizer
from quark.torch.quantization.config.type import Dtype, ScaleType, RoundType, QSchemeType
from quark.torch.quantization.config.config import Config, QuantizationSpec, QuantizationConfig, SmoothQuantConfig
from quark.torch.quantization.observer.observer import PerTensorMinMaxObserver

in_feat = 32 * 128
out_feat = 64 * 128

class MySubModule(nn.Module):
    def __init__(self):
        super().__init__()

        self.layer_norm = nn.LayerNorm(in_feat, bias=False)
        self.lin1 = nn.Linear(in_feat, out_feat, bias=False)
        self.lin1.weight.data = torch.normal(0, 1, (out_feat, in_feat))

    def forward(self, x):
        x = self.layer_norm(x)
        x = self.lin1(x)
        return x

class MyModel(nn.Module):
    def __init__(self):
        super().__init__()

        # We put the Linear + LayerNorm in a ModuleList, which is expected by Quark,
        # as the implementation is tailored for multi-layer transformer models.
        self.layers = nn.ModuleList([MySubModule() for i in range(1)])

    def forward(self, x):
        for layer in self.layers:
            x = layer(x)
        return x

model = MyModel()
model = model.eval()
model_copy = copy.deepcopy(model)

# Create reference tensor with long tail.
inp = torch.empty(1, in_feat)
inp.cauchy_(sigma=5e-3)
inp = inp + torch.normal(0, 1, (out_feat, in_feat))

# Save the reference output.
with torch.no_grad():
    res_orig = model(inp)

# Quantize the model using smoothquant.
quant_spec = QuantizationSpec(
    dtype=Dtype.int8,
    qscheme=QSchemeType.per_tensor,
    observer_cls=PerTensorMinMaxObserver,
    symmetric=False,
    scale_type=ScaleType.float,
    round_method=RoundType.half_even,
    is_dynamic=False,
    ch_axis=None,
    group_size=None
)
global_config = QuantizationConfig(weight=quant_spec, input_tensors=quant_spec)
quant_config = Config(global_quant_config=global_config)

pre_quant_optimization = SmoothQuantConfig(
    scaling_layers=[{"prev_op": "layer_norm", "layers": ["lin1"], "inp": "lin1"}],
    model_decoder_layers="layers",
    alpha=0.5,
    scale_clamp_min=1e-12,
)
quant_config.pre_quant_opt_config.append(pre_quant_optimization)

quantizer = ModelQuantizer(quant_config)
calib_dataloader = DataLoader([{"x": inp}])

quant_model_smooth = quantizer.quantize_model(model, calib_dataloader)
quant_model_smooth = quant_model_smooth.eval()

with torch.no_grad():
    res_quant_smooth = quant_model_smooth(inp)

# Quantize the model without using smoothquant.
quant_config = Config(global_quant_config=global_config)

quantizer = ModelQuantizer(quant_config)

quant_model_nonsmooth = quantizer.quantize_model(model_copy, calib_dataloader)
quant_model_nonsmooth = quant_model_nonsmooth.eval()

with torch.no_grad():
    res_quant_nonsmooth = quant_model_nonsmooth(inp)

print("L1 error non-smooth:", (res_orig - res_quant_nonsmooth).abs().mean())
print("L1 error smooth:", (res_orig - res_quant_smooth).abs().mean())

Giving:

L1 error non-smooth: 3.3892
L1 error smooth: 1.5210

We see that applying SmoothQuant reduces the output error, compared to the reference non-quantized model. Beware that this may not always be the case though, and where SmoothQuant is applied as well as which alpha hyperparameter to used needs to be tuned.

It is easy to check the difference in the weight and activation distribution before and after applying SmoothQuant:

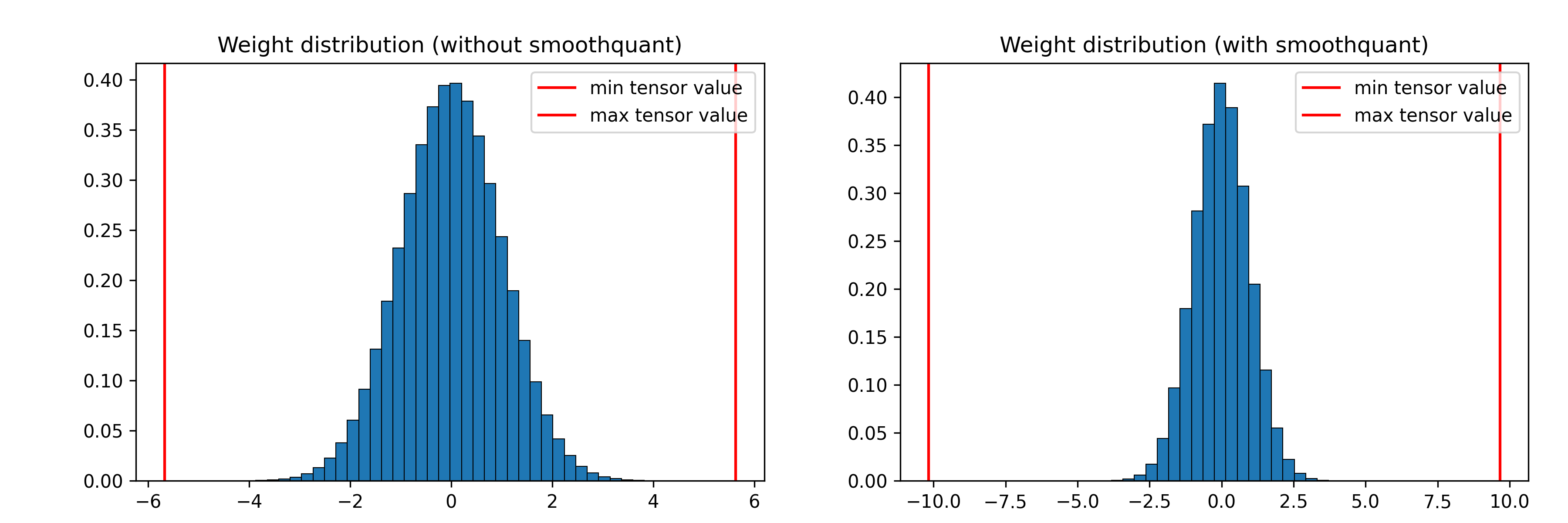
../_images/weight.png — Weight quantization is originally easy (weights well spaced over all quantization bins).#

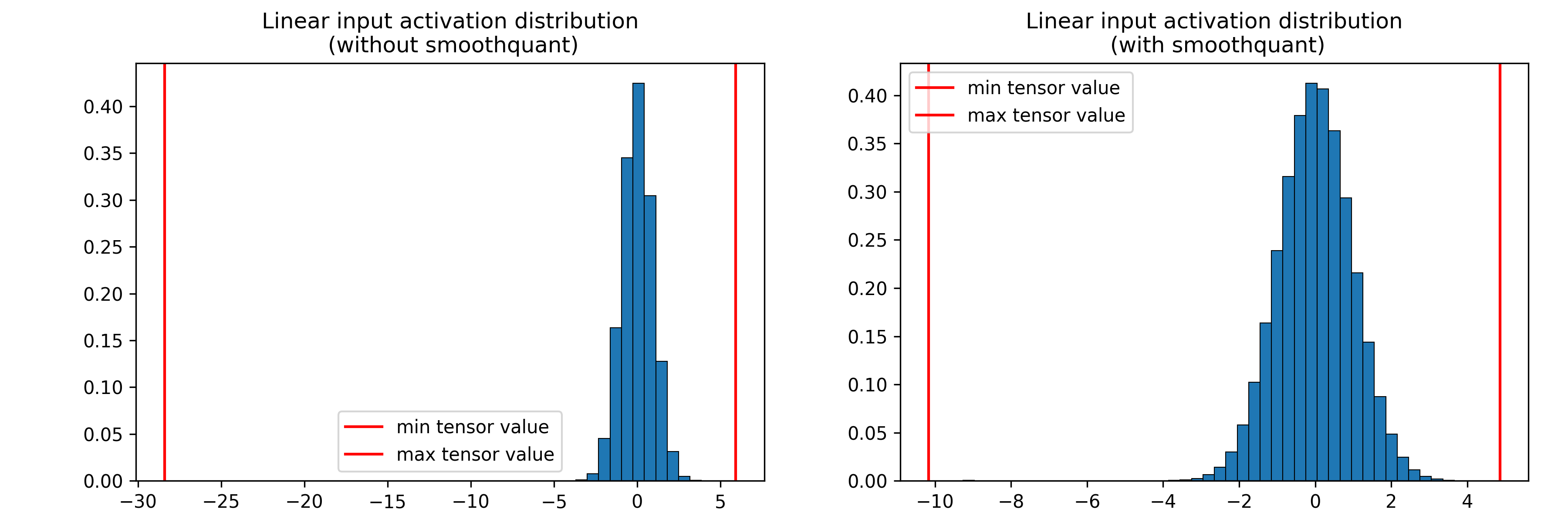
../_images/activation.png — Activation distribution is originally “hard” (activations distribution very narrow, will not be using many quantization bins).#

As seen on the figures, we can afford increasing weight quantization relative error, decreasing activation quantization relative error, with the benefit of overall decreasing the output error compared to the reference model.

Using SmoothQuant in `quark.torch`#

The implementation of SmoothQuant in Quark is designed for LLM models. One needs to define a pre-processing configuration:

from quark.torch.quantization.config.config import SmoothQuantConfig, Config

smoothquant_config = SmoothQuantConfig(
    scaling_layers=[{"prev_op": "layer_norm", "layers": ["lin1"], "inp": "lin1"}],
    model_decoder_layers="layers",
    alpha=0.5,
    scale_clamp_min=1e-12,
)

# There may be several pre-quantization optimization, hence the list.
quant_config = Config(..., pre_quant_opt_config=[smoothquant_config])

The key scaling_layers is a list of dictionaries, each dictionary corresponding to one linear module in the model to apply SmoothQuant on, with:

prev_op: The previous operator to fuse the activation scaling factor \(\frac{1}{s}\) into.
layers: The list of linear layer (or layers) to apply SmoothQuant on. There may be several in case several layers have a common prev_op parent layer (for example: q_proj, k_proj, v_proj in a transformer).
inp: One of layers.

The key model_decoder_layers is the named of a ModuleList module holding the layers in the model.

Examples of such configs can be found in quark/examples/torch/language_modeling/llm_ptq/models. Here is an example for Transformers’ implementation of OPT:

{
    "name": "smooth",
    "alpha": 0.5,
    "scale_clamp_min": 1e-3,
    "scaling_layers":[
        {
            "prev_op": "self_attn_layer_norm",
            "layers": ["self_attn.q_proj", "self_attn.k_proj", "self_attn.v_proj"],
            "inp": "self_attn.q_proj",
        },
        {
            "prev_op": "self_attn.v_proj",
            "layers": ["self_attn.out_proj"],
            "inp":"self_attn.out_proj"
        },
        {
            "prev_op": "final_layer_norm",
            "layers": ["fc1"],
            "inp": "fc1"
        }
    ],
    "model_decoder_layers": "model.decoder.layers"
}

Activation/weight smoothing (SmoothQuant)

Contents

Activation/weight smoothing (SmoothQuant)#

How does SmoothQuant work?#

Using SmoothQuant in quark.torch#

Using SmoothQuant in `quark.torch`#