Quantization with Quark#
What Is Quantization?#
Quantization refers to the process of compressing a numerical value from a higher bit width representation to a lower bit width representation, thereby optimizing memory usage and computational efficiency.
To illustrate this concept, consider the number 1024.
When represented as a typical integer value, which occupies 32 bits or 4 bytes, its memory representation appears as follows:
In this representation, more than 2 bytes of memory (specifically, bits 31 to 11) are allocated to store zeros. By converting this number to a 16-bit integer type, you can achieve the same representation without any loss of information, effectively halving the memory usage:
This process exemplifies quantization. When applied to neural networks, quantization enables the deployment of smaller models that can operate on more cost-effective hardware, potentially at faster speeds than their original, full-sized counterparts.
However, the process is not always straightforward.
Numerical values are often expressed in decimal format, typically adhering to the IEEE-754 floating-point standard. This complexity means that simply removing a few bytes from these data types is not feasible.
To further elucidate, consider representing the number 1024 in a 32-bit floating-point format:
In this format, it becomes less apparent where bits can be removed to compress the value effectively.
There are several critical considerations when performing quantization:
Quantization may result in lossy compression, where precision is irretrievably lost. For instance, a value like 1024.23 might need to be approximated to 1024.0 or 1024.5 at a reduced bit width.
Arithmetic operations involving quantized values may lead to overflow, necessitating a larger bit width to accommodate the result. For example, while 255 can be represented in 8 bits (
1111 1111), the product 255*2 = 510 requires 9 bits (1 1111 1110).A variety of data types are available for quantization, ranging from 16 to 4-bit integers, 16 to 4-bit floating points, and even more advanced composite types like MX.
Given these complexities, utilizing a library such as Quark is advantageous, as it adeptly manages these intricate details on your behalf.
Model Quantization#
In the case of deep learning models, quantization involves converting the weights and activations of the model from floating-point representation to a lower bit width float or integer representation. This transformation can substantially reduce the model’s memory footprint and computational demands, thereby enhancing its efficiency on hardware that supports these lower bit width data types. While quantization can affect model accuracy, the key to successful quantization lies in striking a balance between accuracy and performance.
Model quantization techniques can be broadly classified into two categories:
Quantization-aware training (QAT): This approach integrates quantization into the training process to minimize the accuracy loss that may occur due to quantization.
Post-training quantization (PTQ): This method applies quantization to the model after training, without necessitating retraining.
PTQ is a favored method for quantizing pre-trained models because it does not require retraining and can be applied to any pre-trained model. However, it may lead to a reduction in model accuracy due to the quantization process. Quark assists in restoring model accuracy that might be compromised after quantization by employing various post-training quantization techniques.
The quantization representation of the model can be broadly classified into two categories:
Quantization to low bit float precision: This involves converting from float32 to float16, bfloat16, or float8. In this case, the data remains in a similar floating-point format but with a reduced bit width, which can be advantageous when the hardware supports these lower bit width floating-point data types.
Quantization to integer precision: This involves converting from float32 or float16 to int8 or int4. Here, the data is mapped into an integer data range, which can be beneficial when the hardware supports integer data types and can perform operations on them more efficiently than on floating-point data types.
Considerations for Quantization#
When thinking about quantization, keep these factors in mind:
Target Hardware: Different hardware, like CPUs or GPUs, may handle low-precision calculations differently. Make sure to choose a quantization method that works well with your hardware.
Model Characteristics: The type and complexity of your model can affect how well it handles quantization. More complex models might deal with quantization better than simpler ones.
Use Case Requirements: Different applications have different needs when it comes to accuracy. Knowing what your specific use case requires will help you pick the right quantization method.
Integer Quantization#
Mapping real numbers to integers involves calculating quantization parameters, known as scale and offset. These parameters are represented by the following equations:
Quantization:
q = round(r/s + z)
Dequantization:
r = (q - z) * s
In these equations, ‘q’ is the quantized value, ‘r’ is the real value, ‘s’ is the scale, and ‘z’ is the offset.
To compute these quantization parameters, you observe the real values of the tensor and determine its minimum and maximum values. The scale and offset are then calculated based on these values.
Quark offers various algorithms that help you adjust these quantization parameters to achieve the desired balance between accuracy and performance.
Quantization can be classified based on the offset value:
Symmetric quantization: where z = 0
Asymmetric quantization: where z is not equal to 0
Additionally, quantization can be categorized as per-tensor, per-channel, or per-group, depending on how the quantization parameters (scale and offset) are calculated for the elements of the tensor.
Quark supports different quantization schemes across various frameworks. For more details, refer to the Quark PyTorch/ONNX user guide.
Fake Quantization#
To simplify the manipulation of quantized models and support data types that may not have hardware-level support, Quark uses a technique called simulated quantization, also known as fake quantization.
When you perform quantization in Quark, the values are not directly quantized; instead, they undergo fake quantization.
What Does This Mean?#
This means that values are not immediately converted to their new quantized data types. For example, a 32-bit weight is not stored as an 8-bit integer in memory right away. Instead, it remains in its original bit width for the time being.
The quantization is simulated by compressing the value and then decompressing it back to its original width. The result is at the original bit width, but the value itself can be represented by a lower bit width data type.
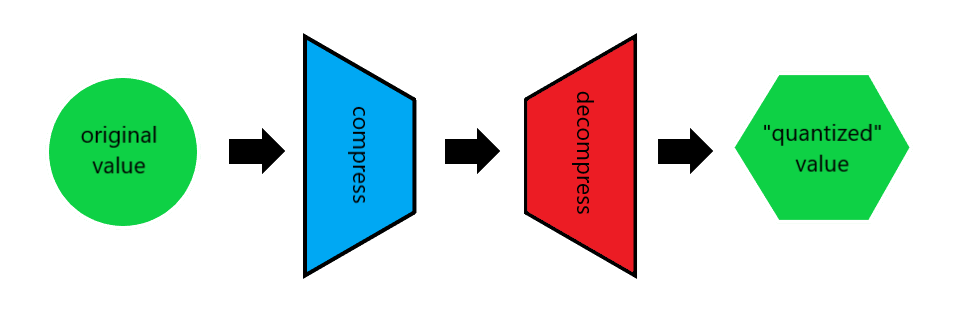
This approach allows you to perform inference on the quantized model in Quark at the higher bit width, so no hardware support for the quantized data type is needed. However, the results will reflect the accuracy you can expect when the quantization is finalized.
When Are Values Actually Converted into Their Quantized Data Types?#
In the PyTorch quantization libraries, quantization is explicitly applied through a function call.
Quark, on the other hand, is designed to export what is known as a QDQ (Quantize-DeQuantize) model.
For instance, if the unquantized model contains the following nodes:
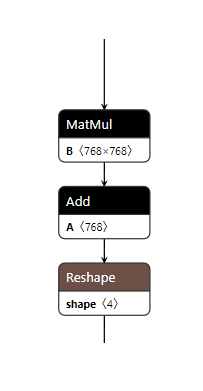
The quantized model exported from Quark might appear like this:
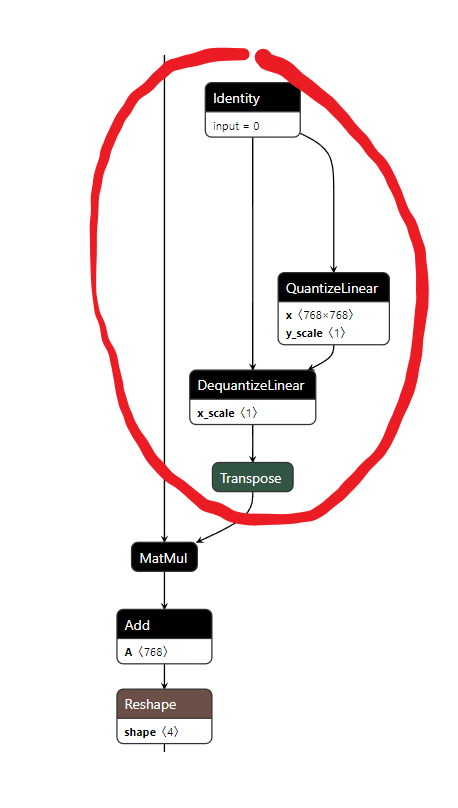
In this model, explicit quantize and dequantize nodes are inserted. The weights and other parameters remain in their original unquantized form, but these new nodes simulate the fake quantization process.
This approach means that any tool consuming this model later will need to collapse the nodes and finalize the quantization. However, a key advantage is that the model can run as is, even without Quark installed at this stage.
What Happens Internally in Quark When We Quantize Something?#
When you pass a model into Quark for quantization, one of the initial steps is replacing certain layers with Quark equivalents.
Currently, there are alternative quantized layers for:
Linear
Conv2d
When Quark encounters either of these layer types, it substitutes them with a Quant version, such as QuantLinear or QuantConv2d.
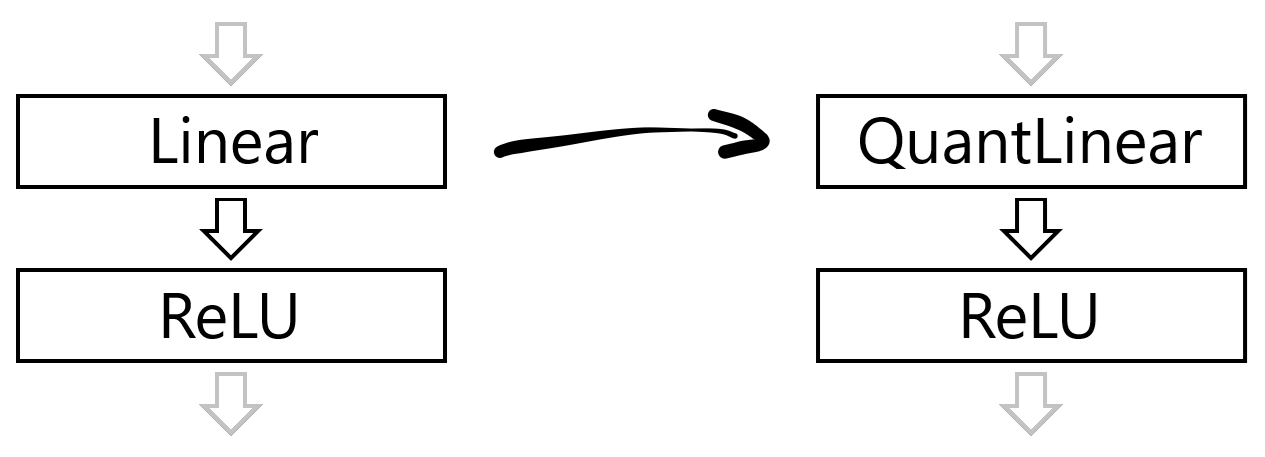
Depending on the selected quantization configuration, these new layers can intercept the inputs, outputs, biases, and weights with fake quantized versions.
The calibration data provided to Quark during the initialization of the quantizer is then passed through the model.
A user-definable observer, such as:
PerTensorMinMaxObserver
PerChannelMinMaxObserver
PerBlockMXObserver
is fed this data as it traverses the model to calculate representative minimum and maximum values needed to correctly quantize the data.