Rotation pre-processing optimization#

A popular line of research (QuaRot, SpinQuant and many others ) has looked into applying rotation matrices to language models weights and activations, with the goal of reducing outliers and improving accuracy recovery from quantization.

To illustrate the idea, consider the vector \((1, 10) \in \mathbb{R}^2\), which has an outlier value of \(10\). With the vector rotated by 45 degrees clockwise, we obtain \((7.7782, 6.3640)\); the values are closer together, effectively removing the outlier. In rotation-based quantization, this idea is applied to tensors that are much larger than \(\mathbb{R}^2\) vectors.

Specifically, a rotation matrix is inserted before quantization, and its inverse is applied after quantization. Thus, at a floating-point level, the network remains unchanged, but the quantized network may achieve much better accuracy.

Consider a linear layer, say

\[z = y W_2\]

where \(y\) is an activation of shape (batch_size, in_features) and \(W_2\) is a weight of shape (in_features, out_features).

This is equivalent to

\[z = (y \times R^{-1}) \times (R \times W_2)\]

where \(R\) is an (in_features, in_features) invertible matrix. After quantization, we get:

\[z \approx \text{quantize}(y \times R^{-1}) \times \text{quantize}(R \times W_2)\]

where \(R\) is fused in the original weight \(W_2\), While the matrix \(R^{-1}\) may be applied online or fused into a preceding layer, e.g.

\[z = (x \times (W_1 \times R^{-1})) \times (R \times W_2).\]

The matrix \(R\) is typically chosen to be an orthogonal matrix (or rotation) that satisfies \(R^T R = R R^T = I\), i.e. \(R^{-1} = R^T\).

AMD Quark supports several rotation settings, that can be applied as a pre-processing step prior to quantization (e.g. with a basic round-to-nearest, or GPTQ, or AWQ, or others). Rotations be parameterized thanks to the RotationConfig configuration.

QuaRot: hadamard rotations#

QuaRot algorithm uses specifically Hadamard matrices for rotations.

An \(n \times n\) Hadamard matrix is an orthogonal matrix of the form \(\frac{1}{\sqrt{n}}A\), where the entries of \(A\) are all \(1\) and \(-1\) (see QuaRot: Outlier-Free 4-Bit Inference in Rotated LLMs). Hadamard rotations are a standard choice for rotation matrices, and Hadamard transforms can often be accelerated using hardware-optimized kernels. In 2D, there are four Hadamard rotations: 45 degrees and 135 degrees clockwise, and 45 degrees and 135 degrees counterclockwise.

QuaRot inserts four fundamental rotations into the model, called R1, R2, R3, and R4 (see SpinQuant: LLM Quantization with Learned Rotations):

R1 and R2 are offline rotations incorporated directly into the model’s weights. R3 and R4 are online operations. They incur a small performance overhead since new operations are added into the model’s computation graph. However, using kernels for fast Hadamard transforms, these operations can be accelerated if necessary.

In detail (reference: SpinQuant paper):

R1: Rotation for the query, key, value projections inputs, as well as the MLP first projection.
R2: Rotation for the attention output projection.
R3: Rotation for the attention queries and keys. It is only useful when performing KV cache quantization.
R4: Rotation for the last MLP projection input.

QuaRot application in AMD Quark#

AMD Quark supports QuaRot algorithm for Llama models by default. An example of usage is available through the quantize_quark.py script.

For example, to quantize Llama 3-8B, both weights and activations, to int8 per tensor while applying QuaRot algorithm to perform rotations before quantization, navigate to quantize_quark.py and run:

python quantize_quark.py \
   --model_dir meta-llama/Meta-Llama-3-8B \
   --quant_scheme int8 \
   --quant_algo rotation

Here are the results for the perplexity of the quantized model Llama-3-8B, with and without Quarot:

Quantization Strategy	Algorithm	Perplexity (Wikitext-2)
no quantization		6.13908052444458
w_int8_per_tensor static quantization	N/A	6.622321128845215
w_int8_per_tensor static quantization	QuaRot (R1+R2 only)	6.181324005126953
w_int8_a_int8_per_tensor static quantization	N/A	253.269912719726
w_int8_a_int8_per_tensor static quantization	QuaRot	6.6984167098999

Here is an example of creating a QuaRot configuration file for an LLM such as Qwen, which has a standard decoder-only transformer architecture:

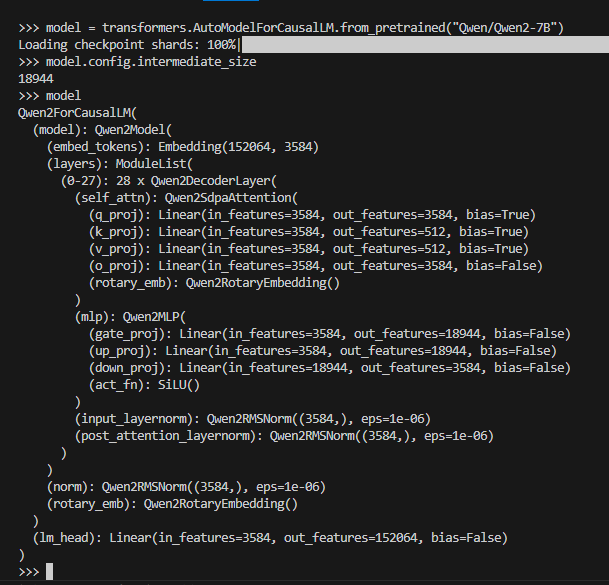
The V and O projections in the attention block can be accessed as layer.self_attn.v_proj and layer.self_attn.o_proj, respectively, for every layer in the list model.layers.

However, notice that the number of input features to the down-projection (intermediate-size) is \(18944 = 148*2^7\). AMD Quark currently only supports \(n \times n\) Hadamard matrices when \(n = m \times 2^k\), where \(m\) is in \({4, 12, 20, 40, 36, 52, 60, 108, 140, 156, 172}\) and \(k >= 0\). Therefore, the online R4 rotation cannot be performed in this case. Instead, perform only the offline operations of R1 and R2 by setting the online-had flag to False. Use the following configuration:

 {
    "name": "quarot",
    "backbone": "model",
    "model_decoder_layers": "model.layers",
    "r1": true,
    "r2": true,
    "r3": false,
    "r4": false,
    "v_proj": "self_attn.v_proj",
    "o_proj":"self_attn.o_proj",
    "self_attn": "self_attn"
}

Here are the results for the perplexity of the quantized model Qwen2-7B, with and without quarot:

Quantization Strategy	Algorithm	Perplexity (Wikitext-2)
no quantization		7.891325950622559
w_int8_per_tensor static quantization	N/A	8.883856773376465
w_int8_per_tensor static quantization	QuaRot (R1+R2 only)	7.948962688446045
w_int8_a_int8_per_tensor static quantization	N/A	172.43882751464844
w_int8_a_int8_per_tensor static quantization	QuaRot (R1+R2 only)	123.24969482421875

Note that QuaRot (and rotations in general) can be combined with other pre-processing algorithms as SmoothQuant or AutoSmoothQuant.

Application example: W8A8 quantization applying SmoothQuant and R1 rotation#

Weight INT8 and Activation INT8 symmetric post-training quantization (W8A8) is one of the most common quantization methods supported by current hardware. It is highly compatible with hardware acceleration, facilitating efficient deployment on various platforms.

The following are the four most common quantization strategies for W8A8:

Weight INT8 (per tensor) activation INT8 (per tensor) static quantization
Weight INT8 (per channel) activation INT8 (per tensor) static quantization
Weight INT8 (per channel) activation INT8 (per tensor) dynamic quantization
Weight INT8 (per channel) activation INT8 (per token) dynamic quantization

Among others, AMD Quark-Torch supports two pre-optimizations that are suitable for W8A8 quantization:

Activation/weight smoothing (SmoothQuant). For more details, see here.
Rotation (R1 in SpinQuant with Hadamard matrix)

It is possible to combine these two methods by smoothing Linear-Linear patterns (Smooth_fc_fc) in decoder layers and rotating RSMNorm-Linear patterns.

Results#

In this example, meta-llama/Meta-Llama-3.1-8B-Instruct is used. All linear layers, excluding lm_head, are quantized using the pre-trained Float16 model (original Float16 model perplexity: 7.2155).

Quantization Strategy	Smooth(alpha=0.85)	Smooth(alpha=0.5)	Smooth_fc_fc(alpha=0.5) + Rotation
w_int8_per_tensor_a_int8_per_tensor static quantization		19.42	8.58
w_int8_per_channel_a_int8_per_tensor static quantization	8.37	15.95	8.40
w_int8_per_channel_a_int8_per_tensor dynamic quantization	9.08	23.35	9.22
w_int8_per_channel_a_int8_per_token dynamic quantization	7.35	7.29	7.27
w_int8_per_tensor_a_int8_per_tensor_kv_cache_int8_per_tensor static quantization		20.51	8.58
w_int8_per_channel_a_int8_per_tensor_kv_cache_int8_per_tensor static quantization	8.38	16.87	8.42
w_int8_per_channel_a_int8_per_tensor_kv_cache_int8_per_tensor dynamic quantization	9.09	23.46	9.26
w_int8_per_channel_a_int8_per_token_kv_cache_int8_per_token dynamic quantization	7.35	7.29	7.28

‘-’ means perplexity > 30

SpinQuant: training orthogonal rotations#

AMD Quark supports training rotations, similar to the approach in SpinQuant and many others and OSTQuant.

The core idea is to train the equivalent (non-destructive) transform \(RR^{-1} = RR^T = I\) that is inserted before quantization of weights and activations, where \(R\) is an orthogonal matrix. Taking the linear layer \(y = xW^T\), we get:

\[\begin{split}y &= xW^T \\ &= xRR^{-1}W^T \\ &= xRR^TW^T \\ &= xR \times (WR)^T \\\end{split}\]

where the activation rotation \(R\) may be fused into a preceding layer, or kept online.

A fully reproducible example is available at amd/Quark, with a few example results.

The core idea brought forward in SpinQuant paper is that trained orthogonal rotations may perform better than random hadamard matrices to reduce the quantization error. We experimentally validate this idea, and support:

Training fully offline rotations (fused into preceding layer, and layer weight).
Training online rotations.

For online rotations, we focus on training block diagonal rotations to limit the computation overhead, as introduced in LightRot <https://ieeexplore.ieee.org/document/10950449/>_ .

The current implementation has been validated for the following model architectures:

Llama3
Qwen3
Qwen3-MOE
GPT OSS

Please refer to the example at amd/Quark, and to the documentation at RotationConfig.

Training SmoothQuant scales#

It is possible to jointly train SpinQuant rotations and SmoothQuant scales. In this case, we train an online transform \(O\) parameterized as:

\[O = DR\]

where \(D\) is a diagonal matrix (SmoothQuant scales), and \(R\) is an orthogonal matrix. Thus, in a linear layer, considering online rotations, we get:

\[\begin{split}y &= xW^T \\ &= xOO^{-1}W^T \\ &= xDRR^TD^{-1}W^T \\ &= xDR \times (WD^{-1}R)^T \\ &= ... x'R \times (WD^{-1}R)^T\end{split}\]

fusing \(D\) into a preceding layer (e.g. RMSNorm weight, or linear weight). The activation rotation \(R\) is here left online.

Adding quantization in, we get:

\[y = \text{quantize}(x'R) \times \text{quantize}(WD^{-1}R)^T.\]

In case we would like to use offline rotations, the transform \(O = RD\) needs to be used instead.