Rotation-based quantization with QuaRot

QuaRot is a rotation-based quantization method that inserts rotation matrices into a model to reduce outliers. Reducing outliers has the effect of significantly improving quantization accuracy. To explain the idea, consider the vector [1, 10]. This has an “outlier”, 10. If we rotate it by 45 degrees clockwise, we get [7.7782, 6.3640]: the values are closer together, the “outlier” removed. In rotation-based quantization we apply this idea to tensors that are much larger than 2x1 vectors. To be precise, we insert a rotation matrix before quantization, and its inverse after quantization. Thus at a floating point level the network is unchanged, but the quantized network should have much better accuracy.

The QuaRot method uses Hadamard matrices for rotations. An \(n x n\) Hadamard matrix is an orthogonal matrix of the form \(\frac{1}{sqrt{n}}A\), where the entries of \(A\) are all \(1\) and \(-1\) (see QuaRot: Outlier-Free 4-Bit Inference in Rotated LLMs). Hadamard rotation are a standard choice for rotation matrices and Hadamard transforms can often be sped up by hardware-optimized kernels. In 2D, there are 4 Hadamard rotations: 45 degrees and 135 degrees clockwise, and 45 degrees and 135 degrees counterclockwise.

QuaRot inserts 4 fundamental rotations into the model: we call these rotations as R1, R2, R3 and R4 (see SpinQuant: LLM quantization with learned rotations). R1 and R2 are offline rotations, and are incorporated directly into the weights of the model. R3 and R4 are online operations. They incur a small performance overhead since we are adding new operations into the graph of the model. But using kernels for fast Hadamard transforms, these can be sped up if necessary.

As we can see, R3 and R4 are online operations. R3 is only needed if we are doing KV cache quantization, and R4 is only needed if we are doing activation quantization.

Quark supports the QuaRot method for Llama models by default, and can be run in one line with the quantize_quark.py script. For example, let’s say that we want to quantize Llama 3-8B, both weights and activations, to int8 per tensor, and we want to apply the QuaRot method so that we perform rotations before quantization. Then we can navigate to the folder examples/torch/language_modeling/llm_ptq and run:

python quantize_quark.py --model_dir meta-llama/Meta-Llama-3-8B --quant_scheme w_int8_a_int8_per_tensor_sym --pre_quantization_optimization quarot

Here are the results for the perplexity of the quantized model Llama-3-8B, with and without quarot:

Quantization Strategy	Algorithm	Perplexity (Wikitext-2)
no quantization		6.13908052444458
w_int8_per_tensor static quantization	N/A	6.622321128845215
w_int8_per_tensor static quantization	QuaRot (R1+R2 only)	6.181324005126953
w_int8_a_int8_per_tensor static quantization	N/A	253.269912719726
w_int8_a_int8_per_tensor static quantization	QuaRot	6.6984167098999

Let us see an example of creating a QuaRot config file for an LLM such as Qwen, which has a standard decoder-only transformer architecture. Let’s take a look:

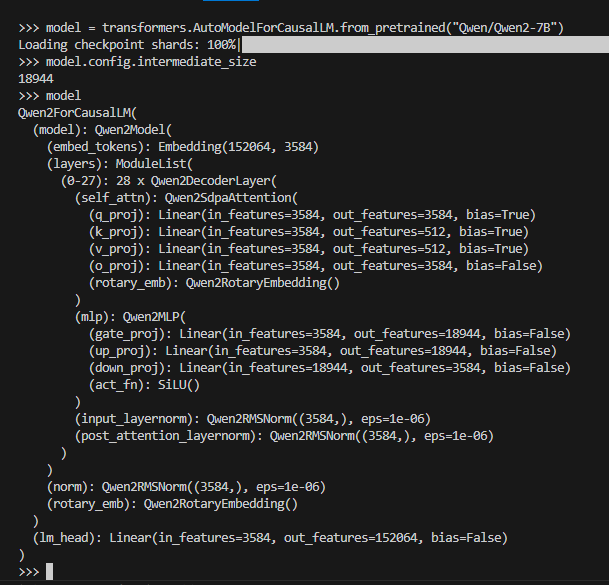
As we can see, the V and O projections in the attention block can be accessed as layer.self_attn.v_proj and layer.self_attn.o_proj, respectively, for every layer in the list model.layers. However, notice that the number of input features to the down-projection (intermediate-size) is \(18944 = 148*2^7\). Quark currently only supports \(n x n\) Hadamard matrices when \(n = m * 2^k\), where \(m\) is in \({4, 12, 20, 40, 36, 52, 60, 108, 140, 156, 172}\) and \(k >= 0\). So we cannot perform the online R4 rotation in this case. So let us only do the offline operations of R1 and R2: we’ll set the online-had flag to False. Let’s use the following config then:

 {
    "name": "quarot",
    "online-had": false,
    "backbone": "model",
    "model_decoder_layers": "model.layers",
    "v_proj": "self_attn.v_proj",
    "o_proj":"self_attn.o_proj",
    "self_attn": "self_attn"
}

Here are the results for the perplexity of the quantized model Qwen2-7B, with and without quarot:

Quantization Strategy	Algorithm	Perplexity (Wikitext-2)
no quantization		7.891325950622559
w_int8_per_tensor static quantization	N/A	8.883856773376465
w_int8_per_tensor static quantization	QuaRot (R1+R2 only)	7.948962688446045
w_int8_a_int8_per_tensor static quantization	N/A	172.43882751464844
w_int8_a_int8_per_tensor static quantization	QuaRot (R1+R2 only)	123.24969482421875

To further improve W8A8 quantization, we might combine QuaRot with SmoothQuant.